自学教程：深度学习: 卷积层的权值和梯度的更新详细说明

权值更新

在前面的反向传播中我们计算出每一层的权值W和偏置b的偏导数之后，最后一步就是对权值和偏置进行更新了。

在之前的BP算法的介绍中我们给出了如下公式：

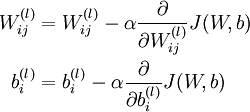
其中的α为学习速率，一般学习率并不是一个常数，而是一个以训练次数为自变量的单调递减的函数。使用变化的学习率有以下几点理由：

1、开始时学习率较大，可以快速的更新网络中的参数，是参数可以较快的达到目标值。而且由于每次更新的步长较大，可以在网络训练前期“跳过”局部最小值点。

2、当网络训练一段时间后，一个较大的学习率可能使网络的准确率不再上升，即“网络训练不动”了，这时候我们需要减小学习率来继续训练网络。

在我们的网络中，含有参数的层有卷积层1、卷积层2、全连接层1和全连接层2，一共有4个层有参数需要更新，其中每个层又有权值W和偏置b需要更新。实际中不管权值还是偏置，还有我们前面计算出了的梯度，都是线性存储的，所以我们直接把整个更新过程用到的数据看作对一维数组就可以，不用去关注权值W是不是一个800*500的矩阵，而且这样的话，权值更新和偏置更新的具体实现可以共用一份代码，都是对一维数组进行操作。

权值更新策略

caffe中的学习率更新策略

在\src\caffe\solvers\sgd_solver.cpp文件的注释中，caffe给出如下几种学习率更新策略：

1. // Return the current learning rate. The currently implemented learning rate  
2. // policies are as follows:  
3. //    - fixed: always return base_lr.  
4. //    - step: return base_lr * gamma ^ (floor(iter / step))  
5. //    - exp: return base_lr * gamma ^ iter  
6. //    - inv: return base_lr * (1 + gamma * iter) ^ (- power)  
7. //    - multistep: similar to step but it allows non uniform steps defined by  
8. //      stepvalue  
9. //    - poly: the effective learning rate follows a polynomial decay, to be  
10. //      zero by the max_iter. return base_lr (1 - iter/max_iter) ^ (power)  
11. //    - sigmoid: the effective learning rate follows a sigmod decay  
12. //      return base_lr ( 1/(1 + exp(-gamma * (iter - stepsize))))  
13. //  
14. // where base_lr, max_iter, gamma, step, stepvalue and power are defined  
15. // in the solver parameter protocol buffer, and iter is the current iteration.  

可以看出，学习率的更新有fixed、step、exp、inv、multistep、poly和sigmoid几种方式，看上边的公式可以很清楚的看出其实现过程。

实际中我们的网络使用的是inv的更新方式，即learn_rate=base_lr * (1 + gamma * iter) ^ (- power)。

Caffe中权值更新的实现

在配置文件\examples\mnist\lenet_solver.prototxt中，保存了网络初始化时用到的参数，我们先看一下和学习率相关的参数。

1. # The base learning rate, momentum and the weight decay of the network.  
2. base_lr: 0.01  
3. momentum: 0.9  
4. weight_decay: 0.0005  
5. # The learning rate policy  
6. lr_policy: "inv"  
7. gamma: 0.0001  
8. power: 0.75  

根据上面的参数，我们就可以计算出每一次迭代的学习率learn_rate= base_lr * (1 + gamma * iter) ^ (- power)。

获取学习率之后，我们需要使用学习率对网络中的参数进行更新。在\src\caffe\solvers\sgd_solver.cpp中包含了进行权值更新的具体函数ApplyUpdate()，下面我们介绍一下这个函数。

1. template <typename Dtype>
2. void SGDSolver<Dtype>::ApplyUpdate() {
3. CHECK(Caffe::root_solver());
4. //GetLearningRate()函数获取此次迭代的学习率
5. Dtype rate = GetLearningRate();
6. if (this->param_.display() && this->iter_ % this->param_.display() == 0) {
7. LOG(INFO) << "Iteration " << this->iter_ << ", lr = " << rate;
8. }
9. ClipGradients();
10. //对网络进行更新，一共4个层，每层有W和b2个参数需要更新，故size=8
11. for (int param_id = 0; param_id < this->net_->learnable_params().size();
12. ++param_id) {
13. //归一化，我们的网络没有用到这一函数
14. Normalize(param_id);
15. //正则化
16. Regularize(param_id);
17. //计算更新用到的梯度
18. ComputeUpdateValue(param_id, rate);
19. }
20. //用ComputeUpdateValue计算得到的梯度进行更新
21. this->net_->Update();
22. }

1. void SGDSolver<Dtype>::Regularize(int param_id) {
2. const vector<Blob<Dtype>*>& net_params = this->net_->learnable_params();
3. const vector<float>& net_params_weight_decay =
4. this->net_->params_weight_decay();
5. Dtype weight_decay = this->param_.weight_decay();
6. string regularization_type = this->param_.regularization_type();
7. // local_decay = 0.0005 in lenet
8. Dtype local_decay = weight_decay * net_params_weight_decay[param_id];
9.  
10. ...
11. if (regularization_type == "L2") {
12. // axpy means ax_plus_y. i.e., y = a*x + y
13. caffe_axpy(net_params[param_id]->count(),
14. local_decay,
15. net_params[param_id]->cpu_data(),
16. net_params[param_id]->mutable_cpu_diff());
17. }
18. ...
19. }

1. void SGDSolver<Dtype>::ComputeUpdateValue(int param_id, Dtype rate) {
2. const vector<Blob<Dtype>*>& net_params = this->net_->learnable_params();
3. const vector<float>& net_params_lr = this->net_->params_lr();
4. // momentum = 0.9 in lenet
5. Dtype momentum = this->param_.momentum();
6. // local_rate = lr_mult * global_rate
7. // lr_mult为该层学习率乘子，在lenet_train_test.prototxt中设置
8. Dtype local_rate = rate * net_params_lr[param_id];
9.  
10. // Compute the update to history, then copy it to the parameter diff.
11.  
12. ...
13. // axpby means ax_plus_by. i.e., y = ax + by
14. // 计算新的权值更新变化值 \delta w,结果保存在历史权值变化中
15. caffe_cpu_axpby(net_params[param_id]->count(), local_rate,
16. net_params[param_id]->cpu_diff(), momentum,
17. history_[param_id]->mutable_cpu_data());
18.  
19. // 从历史权值变化中把变化值 \delta w 保存到历史权值中diff中
20. caffe_copy(net_params[param_id]->count(),
21. history_[param_id]->cpu_data(),
22. net_params[param_id]->mutable_cpu_diff());
23. ...
24. }

1. caffe_axpy<Dtype>(count_, Dtype(-1),
2. static_cast<const Dtype*>(diff_->cpu_data()),
3. static_cast<Dtype*>(data_->mutable_cpu_data()));

在ComputeUpdateValue用到了lr_mult学习率因子参数，这个在之前的配置信息里面也见过，同一层中的weight和bias可能会以不同的学习率进行更新，所以也可以有不同的lr_mult。

最后this->net_->Update()函数使用前边ComputeUpdateValue计算出来的偏导数对参数进行了更新

1. layer {
2. name: "conv2_1/2/conv"
3. type: "Convolution"
4. bottom: "conv2_1/2/pre"
5. top: "conv2_1/2"
6. param {
7. lr_mult: 1.0
8. decay_mult: 1.0
9. }
10. param {
11. lr_mult: 2.0
12. decay_mult: 0.0
13. }
14. convolution_param {
15. num_output: 24
16. weight_filler {
17. type: "xavier"
18. }
19. bias_filler {
20. type: "constant"
21. value: 0.1
22. }
23. pad_h: 1
24. pad_w: 1
25. kernel_h: 3
26. kernel_w: 3
27. stride_h: 1
28. stride_w: 1
29. }
30. }