自学教程：损失函数改进之Large-Margin Softmax Loss

最近几年网络效果的提升除了改变网络结构外，还有一群人在研究损失层的改进，这篇博文要介绍的就是较为新颖的Large-Margin softmax loss（L-softmax loss）。Large-Margin softmax loss来自ICML2016的论文：Large-Margin Softmax Loss for Convolutional Neural Networks
论文链接：http://proceedings.mlr.press/v48/liud16.pdf，
MxNet代码链接：https://github.com/luoyetx/mx-lsoftmax

先来直观看下Large-Margin Softmax Loss的效果，也是论文的核心：

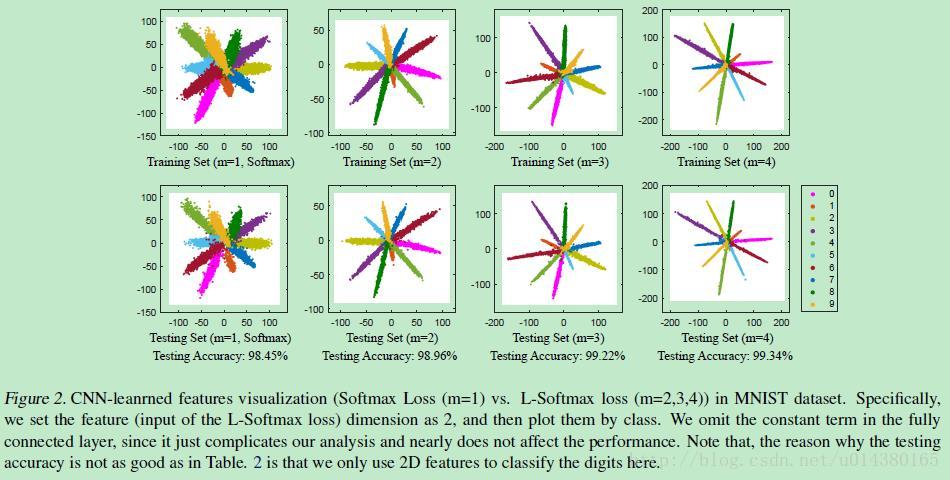
什么意思呢？上面一行表示training set，下面一行表示testing set。每一行的第一个都是传统的softmax，后面3个是不同参数的L-softmax，看看类间和类内距离的差距！

因为L-softmax loss是在原来传统的softmax loss上改进的，因此还是先从softmax loss讲起：
softmax loss的公式如下：

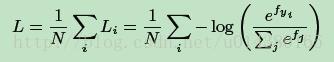
fj表示class score f向量的第j个元素。N表示训练数据的数量。log函数的括号里面的内容就是softmax，（如果不是很理解softmax，softmax loss，可以参看这篇博文：softmax，softmax-loss，BP的解释）简单讲就是属于各个类别的概率，因此fyi就可以理解为全连接层的输出，也就是：

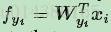
上面这个式子就是W和x的内积，因此可以写成下面这样：

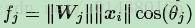
因此Li就变成下式：

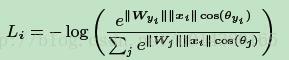
那么Large Margin Softmax Loss是什么意思？
假设一个2分类问题，x属于类别1，那么原来的softmax肯定是希望：

也就是属于类别1的概率大于类别2的概率，这个式子和下式是等效的：

那么Large Margin Softmax就是将上面不等式替换成下式：

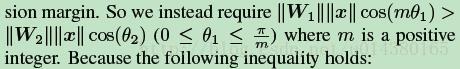
因为m是正整数，cos函数在0到π范围又是单调递减的，所以cos(mx)要小于cos(x)。m值越大则学习的难度也越大，这也就是最开始Figure2中那几个图代表不同m值的意思。因此通过这种方式定义损失会逼得模型学到类间距离更大的，类内距离更小的特征。不过个人认为可能需要迭代次数多点才能看到效果。

这样L-softmax loss的Li式子就可以在原来的softmax loss的Li式子上修改得到：

Figure4是从几何角度直观地看两种损失的差别，L-softmax loss学习到的参数可以将两类样本的类间距离加大。通过对比可以看到L-softmax loss最后学到的特征之间的分离程度比原来的要明显得多。

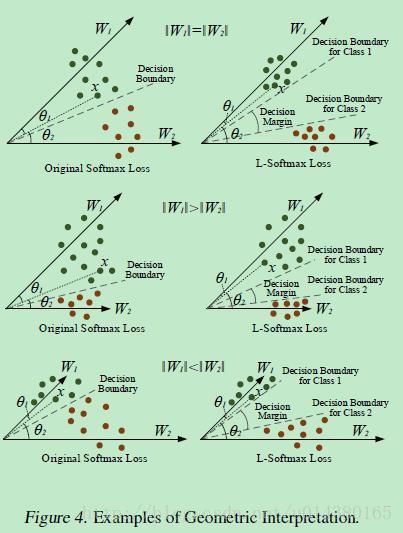
因此L-softmax loss的思想简单讲就是加大了原来softmax loss的学习难度。借用SVM的思想来理解的话，如果原来的softmax loss是只要支持向量和分类面的距离大于h就算分类效果比较好了，那么L-softmax loss就是需要距离达到mh（m是正整数）才算分类效果比较好了。