这篇教程二分类问题的交叉熵损失函数多分类的问题的函数交叉熵损失函数求解写得很实用,希望能帮到您。
二分类问题的交叉熵损失函数;
在二分类问题中,损失函数为交叉熵损失函数。对于样本(x,y)来讲,x为样本 y为对应的标签。在二分类问题中,其取值的集合可能为{0,1},我们假设某个样本的真实标签为yt,该样本的yt=1的概率为yp,则该样本的损失函数为:

如果对于整个数据集上的模型而言:其损失函数就是所有样本的点的损失函数的平均值。
多分类的问题的函数交叉熵损失函数:
在多分类问题中,损失函数也是交叉熵损失函数,对于样本(x,y)来讲,y是真实的标签,预测标签为所有标签的集合,我们假设有k个标签值,第i个样本预测为第K个标签的概率为pi,k,一共有N个样本,则总的数据集损失函数为:
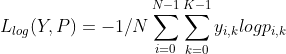
下面是二分类和多分类问题的代码:利用sklearn库编写
from sklearn.metrics import log_loss
#from sklearn.preprocessing import LabelBinarizer
from math import log
y_true = [0,1]
y_pred = [[.48,.52],[.48,.52]]
sk_log_loss = log_loss(y_true,y_pred)
print('Loss by sklearn: %s.'% sk_log_loss)
loss = 0
for lable,prob in zip(y_true,y_pred):
loss -= (lable * log(prob[0])+(1-lable)*log(1-prob[1]))
loss = loss/len(y_true)
print('loss by equation: %s.'%loss)
from sklearn.metrics import log_lossfrom math import log -
-
y_true = [0,0,1,1]y_pred = [[.9,.1],[.8,.2],[.2,.8],[.3,.7]]sk_log_loss = log_loss(y_true,y_pred)print('Loss by sklearn: %s.'% sk_log_loss)-
loss = 0for lable,prob in zip(y_true,y_pred)Loss -= (lable * log(prob[0])+(1-lable)*log(1-prob[1]))Loss = Loss/len(y_true)print('Loss by equation: %s.'%Loss)
from sklearn.metrics import log_lossfrom sklearn.preprocessing import LabelBinarizerfrom math import log-
y_true = ['1', '4', '5'] # 样本的真实标签y_pred = [[0.1, 0.6, 0.3, 0, 0, 0, 0, 0, 0, 0],[0, 0.3, 0.2, 0, 0.5, 0, 0, 0, 0, 0],[0.6, 0.3, 0, 0, 0, 0.1, 0, 0, 0, 0]] # 样本的预测概率labels = ['0','1','2','3','4','5','6','7','8','9'] # 所有标签-
-
# 利用sklearn中的log_loss()函数计算交叉熵sk_log_loss = log_loss(y_true, y_pred, labels=labels)print("Loss by sklearn is:%s." %sk_log_loss)-
# 对样本的真实标签进行标签二值化lb = LabelBinarizer()print(lb.fit(labels))transformed_labels = lb.transform(y_true)print(transformed_labels)#转化代码为矩阵-
N = len(y_true) # 样本个数K = len(labels) # 标签个数-
eps = 1e-15 # 预测概率的控制值Loss = 0 # 损失值初始化-
for i in range(N):for k in range(K):# 控制预测概率在[eps, 1-eps]内,避免求对数时出现问题if y_pred[i][k] < eps:y_pred[i][k] = epsif y_pred[i][k] > 1-eps:y_pred[i][k] = 1-eps# 多分类问题的交叉熵计算公式Loss -= transformed_labels[i][k]*log(y_pred[i][k])-
Loss /= Nprint("Loss by equation is:%s." % Loss)
Softmax机器学习重要的工具详细推导公式和实现代码
深度学习遵循“垃圾入,垃圾出”(“garbage in, garbage out”)的基本法则Andrej Karpathy 在Train AI 演讲:改善数据集 |

