上一节,我们深度优先遍历了搜索树,而没有广度优先遍历。本节介绍的Alpha-Beta搜索,会有力提高搜索算法的效率,并体现出深度优先遍历的优势。Alpha-Beta搜索非常重要,是后面课程的基础。本节课程可以分为以下3步学习:
(1)、学习负极大值搜索。这与上节课程是有关联的,并不难懂。了解负极大值搜索,是为了更容易接受Alpha-Beta搜索。另外,在文件“search - 负极大值搜索.js”中,实现了负极大值搜索。
(2)、理解剪枝的原理,然后学习Alpha-Beta搜索。在文件“search - 一个简单的Alpha-Beta搜索.js”中,实现了一个简单的,不超出边界的Alpha-Beta搜索。
(3)、学习在Alpha-Beta基础上进行的一些优化,包括超出边界的Alpha-Beta搜索、杀棋的分数、历史表启发。
5.1、负极大值搜索
前面介绍了极大点搜索和极小点搜索,两种算法的大部分逻辑是一样的。可以合并这两种算法,合并后就是负极大值搜索算法,搜索树如下:
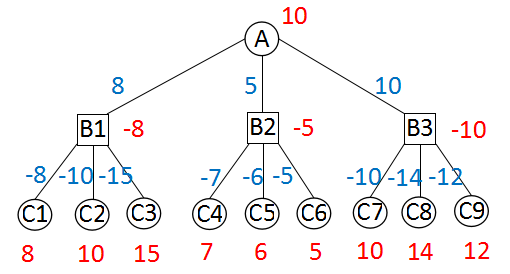
红色数字是当前节点的分值,蓝色数字是父节点对子节点返回值取负后的值。
搜索进行到C1、C2、C3时,要做评估,得到的估值是8、10、15。由于此时轮到红方走棋,表示红方在三个局面分别有8、10、15的优势。在极大极小搜索中,要在B1求这三个局面估值的最小值。现在我们可以这样来看,黑方在C1、C2、C3的优势分别为-8、-10、-15。黑方显然在B1点需要对三个局面做一个选择,选择的目标当然是优势最大化。可以这样表示:
max(-8, -10, -15)
在极大极小搜索中,B1是黑方走棋,是极小点,应该求最小值。现在由于多加了一个负号,也变成求极大值了,B1点也成了极大点。
黑方在B1、B2、B3分别取得了-8、-5、-10的优势,对于红方来讲,则在这三个点分别有8、5、10的优势。所以在A点,轮到红方走棋,它会在B1、B2、B3中选择最大值,即:
max(8, 5, 10)
负极大值搜索伪代码如下:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21 |
Search.prototype.negaMaxSearch = function(depth) {
如果depth等于0,调用评估函数并返回分值
var vlBest = 负无穷; // 初始最优值
var mvs = 当前局面全部走法; // 生成当前局面的所有走法
var value = 0;
for (var i = 0; i < mvs.length; i ++) {
执行招法mvs[i]
value = -this.negaMaxSearch(depth - 1); // 递归调用自身,注意有个负号
撤销招法mvs[i]
if (value > vlBest) { // 寻找最大估值
vlBest = value;
if (depth == MINMAXDEPTH) { // 如果回到根节点,需要记录最佳走法
记录根节点的最佳走法
}
}
}
return vlBest; // 返回当前节点的最优值
} |
在极大极小算法中,叶子节点调用评估函数,始终返回红方优势。根节点如果红方走棋,调用极大点算法;否则调用极小点算法。
在负极大值算法中,所有节点都是极大点。评估函数就不能总是返回红方优势了,应该返回叶子节点走棋方的优势。另外,走棋方具有先走棋的权利,我们认为这是一种优势。为体现这个优势,局面得分加上ADVANCED_VALUE(也就是3)的分值。
评估函数应该修改为:
1
2
3
4
5 |
Position.prototype.evaluate = function() {
var vl = (this.sdPlayer == 0 ? this.vlWhite - this.vlBlack :
this.vlBlack - this.vlWhite) + ADVANCED_VALUE;
return vl;
} |
5.2、浅的搜索剪枝
极大极小搜索以及负极大值搜索,都是对整个搜索树进行完全搜索。实际上,有些没用的分支是可以裁减掉的,这样会大大缩短搜索时间。先来看一个极大极小搜索树(使用负极大值搜索树,道理是一样的。不过极大极小搜索树更直观,更简单一点。):
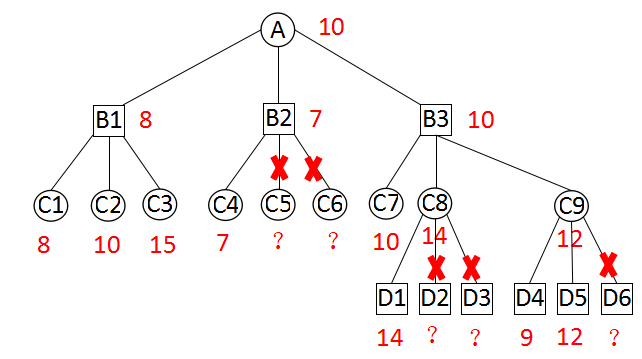
当搜索到B2点时,红方A点已经通过B1的搜索得到了一个当前最优值8,红方希望通过B2这条路径得到更好的值。当搜索到C4时得到一个估值7,也就是B2当前最优值。由于B2是极小点,在搜索B2剩余的子节点时,凡是估值超过7的B2都不会考虑,一旦有值小于7就会取代7成为新的最优值。也就是说,B2的值不超过7。那么对于A点来讲,B2就没有意义,继续搜索B2的后续子节点也毫无意义。C5、C6不必搜索,而直接返回A点,继续A点后续子节点的搜索。
C8、C9节点与B2节点类似,也可以进行剪枝。
以C9节点为例,当搜索到C9时,黑方B3点已经通过对C7、C8的搜索,得到了一个最优值10。当搜索到D5节点是,得到一个估值12。由于C9是极大点,因此C9的值不会低于12。对B3点来说,C9毫无意义,不用再搜索C9的后续节点。
我们再来看一下负极大值搜索树:
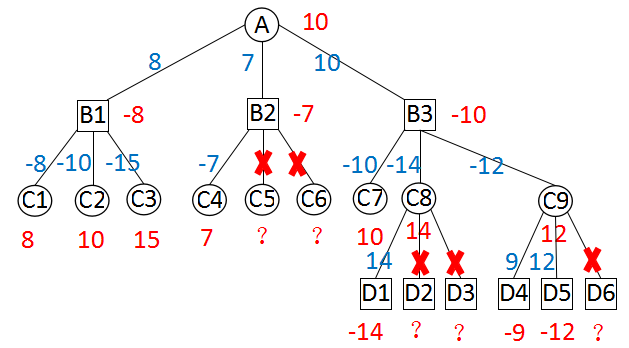
红色数字是当前节点的分值,蓝色数字是父节点对子节点返回值取负后的值。
搜索进行到C1、C2、C3时,得到估值分别是8、10、15,也就是说红方优势分别是8、10、15。那么,这三点黑方优势分别是-8、-10、-15。B1点要在C1、C2、C3点做出抉择,自然会选择黑方优势最大的C1点,B1点估值-8。
在B1点,-8是黑方的优势,那么-8也可以被认为是红方的劣势。红方希望通过对B2的搜索,来减小这一劣势(也就是得到-9、-10之类,小于-8的估值)。搜索完C4后,B2点得到了一个最优值-7。由于目前所有节点都是极大点,B2的估值不会小于-7。B2点增大了红方得的劣势,休想A点选择B2这条路线,对B2剩余子节点的搜索也就毫无意义。
怎样实现这一算法呢?我们再回到B2点。只要把A点已知的红方劣势,也就是-8,传递给B2点,就能实现这一裁剪。A点传递给B2点的这个参数,我们叫做Beta;这一搜索算法,我们叫做Beta搜索。伪代码如下:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25 |
Search.prototype.betaSearch = function(depth, beta) {
如果depth等于0,调用评估函数并返回分值
var vlBest = 负无穷; // 初始最优值
var mvs = 当前局面全部走法; // 生成当前局面的所有走法
var value = 0;
for (var i = 0; i < mvs.length; i ++) {
执行招法mvs[i]
value = -this.betaSearch(depth - 1); // 递归调用自身,注意有个负号
撤销招法mvs[i]
if(value > beta) { // 得到一个大于bate的值,终止对当前节点的搜索
return beta;
}
if (value > vlBest) { // 寻找最大估值
vlBest = value;
if (depth == MINMAXDEPTH) { // 如果回到根节点,需要记录最佳走法
记录根节点的最佳走法
}
}
}
return vlBest; // 返回当前节点的最优值
} |
5.3、深的搜索剪枝
我们来讨论更复杂的可能裁剪的情况,
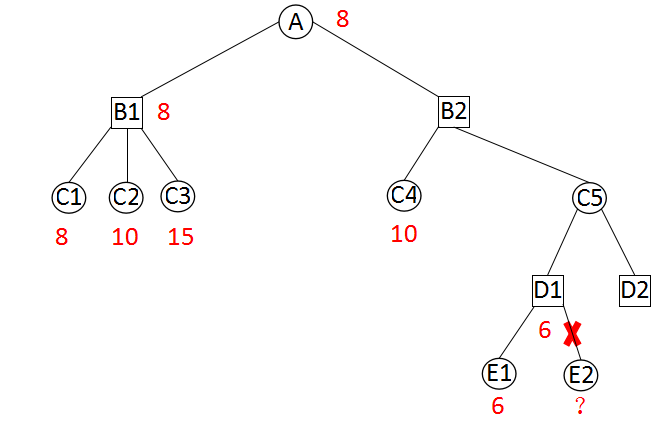
当搜索B2节点时,已知B1节点的估值是8。从B2点向下两层,有个D1点。D1点搜索完E1点后,得到E1的估值为6。由于D1是极小点,D1的估值不大于6。如果从C5点返回6或者更小,那么我们就可以在B2上做裁剪,因为它有更好的兄弟节点 B1(这里的更好是对A点来说的)。因此,继续搜索D1的后续节点毫无意义,E2不必搜索。
为了实现深的裁剪,除了传递参数Beta,我们还要传递一个参数Alpha,这就形成了Alpha-Beta搜索。
5.4、Alpha-Beta搜索
Alpha-Beta搜索与Beta搜索很相似,伪代码如下:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25 |
Search.prototype.alphaBetaSearch = function(vlAlpha_, vlBeta, depth) {
如果depth等于0,调用评估函数并返回分值
var vlAlpha = vlAlpha_; // 初始最优值,不再是负无穷
var mvs = 当前局面全部走法; // 生成当前局面的所有走法
var vl = 0;
for (var i = 0; i < mvs.length; i ++) {
执行招法mvs[i]
vl = -this.alphaBetaSearch(-vlBeta, -vlAlpha, depth - 1); // 递归调用
撤销招法mvs[i]
if(vl >= vlBeta) { // 得到一个大于或等于bate的值,终止对当前节点的搜索
return vlBeta;
}
if (vl > vlAlpha) { // 寻找最大估值
vlAlpha = vl;
if (depth == MINMAXDEPTH) { // 如果回到根节点,需要记录最佳走法
记录最佳走法
}
}
}
return vlAlpha; // 返回当前节点的最优值
} |
在根节点,Alpha取负无穷,Beta取正无穷。当函数递归时,Alpha和Beta不但取负数而且要交换位置。Alpha表示当前搜索节点走棋一方搜索到的最好值,任何比它小的值对当前节点走棋方都没有意义。Beta表示对手目前的劣势,这是对手所能承受的最坏结果。Beta值越大,表示对方劣势越明显;Beta值越小,表示对方劣势也越小。在对手看来,他总是希望找到一个对策不比Beta更坏。如果当前节点返回Beta或比Beta更好的值,作为父节点的对方就绝不会选择这种策略。
5.5、超出边界Alpha-Beta搜索
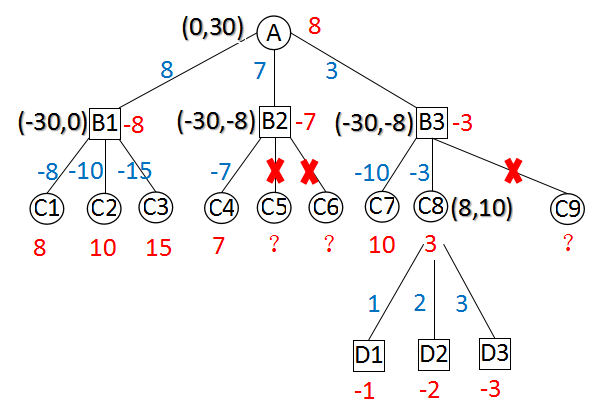
图A 超出边界的Alpha-Beta搜索
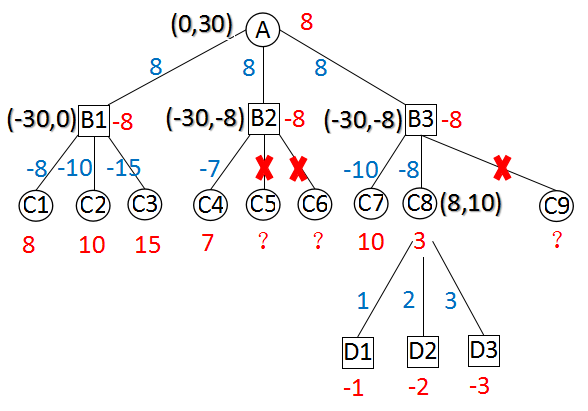
图B 不超出边界的Alpha-Beta搜索
以上两图,分别描述了“超出边界的Alpha-Beta搜索”和“不超出边界的Alpha-Beta搜索”。
括号中的两个值,是当前节点的初始alpha和beta。
从上面两图可以看出,B2点第1种走法得到value = -7,产生剪枝。B2点无论返回-7还是-8都不会影响A点的值。C8的所有走法得到的值均小于8,无论返回3还是8在父节点都会引起剪枝。
不管是哪种搜索方法,最终根节点的搜索结果是一样的,搜索效率也一样。不过,将来程序中会引入置换表(后面的课程会介绍这个概念),超出边界的Alpha-Beta搜索查找置换表时命中率更高,更有优势。因此,程序中直接使用了超出边界的Alpha-Beta搜索。
5.6、杀棋的分数
考虑这样一个搜索树:
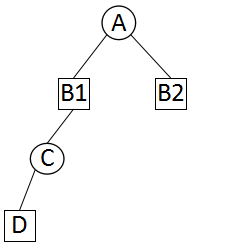
在根节点A点,红方优势明显,即将取得胜利。而在D点和B2点,都是黑方被将死或者困毙的局面。如果D、B2两节点的估值都是-MATE_VALUE(也就是-10000),那么A点沿这两个搜索路径得到的估值都是10000。当估值相同时,我们的程序一般采用前面的走法。但是对红方来说,明显第二个路径更好,一步就能取得胜利。为解决这一问题,可以把输棋的分值,与搜索层数结合起来:
输棋分值 = -MATE_VALUE + 搜索层数
例如,A、B1、B2、C、D的搜索层数分别是0、1、1、2、3。D节点估值
-10000 + 3 = -9997
B2节点估值
-10000 + 1 = -9999
在我们的程序中,使用如下函数实现:
1
2
3 |
Position.prototype.mateValue = function() {
return this.distance - MATE_VALUE;
} |
5.7、历史表启发(History Heuristic)
Alpha-Beta搜索严重依赖于着发的搜索顺序。如果总是先去搜索最坏的着法,那么Beta截断就不会发生,因此该算法就如同极大极小搜索一样,效率非常低。如果程序总是能挑最好的着法来首先搜索,就能不断发生Beta截断,大大提高搜索效率。因此使用Alpha-Beta搜索时,着发顺序至关重要。
国际象棋程序的经验证明,历史表是很好的走法排序依据。什么是历史表呢?如果一个着法在不同层很多节点都被搜索过,并且是很好的走法,那么我们就将该走法存入历史表,并对该走发赋一个值(当然,这个走法被搜索到的次数越多,赋的值就越大)。
什么样的走法算是比较好的走法呢?我们的程序选择了以下两类走法:
1、产生Beta截断的走法
2、不能产生Beta截断,但它是所有PV走法(也就是Beta > vl > vlAlpha的走法)中最好的走法。
历史表historyTable[]是一个大小为4096的数组,遇到一个比较好的走法mv时,给历史表中的该走法增加一个value值:
historyTable[mv] = historyTable[mv] + value
对于value的取值,我们沿用国际的经验——深度的平方。也就是说,
value = depth * depth
事实上,我们的程序并没有按照惯例,使用mv作为历史表的指标,并不存在historyTable[mv]这样的写法。我们使用“棋子类别 + 走法终点位置”作为历史表的指标。我是这样理解这一指标的:比如已知的几个不错的走法,都是将红车移动到某一位置。如果遇到一个走法,也是将红车移动到这一位置,那么我们猜测,这一走法也是个不错的走法。
获取历史表指标的方法如下:
1
2
3 |
Position.prototype.historyIndex = function(mv) {
return ((this.squares[SRC(mv)] - 8) << 8) + DST(mv);
} |
更新历史表的方法如下:
1
2
3 |
Search.prototype.setBestMove = function(mv, depth) {
this.historyTable[this.pos.historyIndex(mv)] += depth * depth;
} |
5.8、迭代加深
上一节的极大极小搜索,搜索深度固定为3。这一节使用了效率更高的Alpha-Beta搜索,完全可以增大搜索深度了。深度太浅,无法充分利用电脑性能;深度过深,又要等待很久的时间。那我们干脆不指定搜索深度了,而是指定搜索时间。设置搜索时间为100毫秒,从深度depth=1开始搜索。如果搜索完后还有时间,那就增加深度继续搜索,伪代码如下:
for (i = 1; i < 最大深度; i ++) {
alphaBetaSearch(负无穷, 正无穷, i); // 搜索深度为i
if (超过搜索时间) {
break;
}
}
迭代加深不仅充分利用了时间资源,还能充分发挥历史表的作用——前一层搜索结束后,将在历史表中积累大量数据,这将有效减少深一层搜索的时间。
5.9、核心代码说明
本节的代码可以在 Github 下载,也可以直接clone
git clone -b step-5 https://github.com/Royhoo/write-a-chinesechess-program
Search中新增或修改的主要属性和方法:
(1)、historyTable[]
该数组是历史表。
(2)、searchMain(depth, millis)
增加了迭代加深搜索。
(3)、alphaBetaSearch(vlAlpha_, vlBeta, depth)
实现了Alpha-Beta搜索,并且:
1、根据杀棋步数给出杀棋分数。
2、使用历史表优化搜索效率。
在文件“search.js”中,新增了一个对象MoveSort,用于生成一个局面排序后的走法。
下载地址:
JavaScript中国象棋程序(6) - 克服水平线效应、检查重复局面
JavaScript中国象棋程序(4) - 极大极小搜索算法 |

