这篇教程小批量随机梯度下降深度学习优化函数详解-- mini-batch SGD 小批量随机梯度下降写得很实用,希望能帮到您。
本文延续该系列的上一篇 深度学习优化函数详解(2)-- SGD 随机梯度下降
上一篇我们说到了SGD随机梯度下降法对经典的梯度下降法有了极大速度的提升。但有一个问题就是由于过于自由 导致训练的loss波动很大。那么如何可以兼顾经典GD的稳定下降同时又保有SGD的随机特性呢?于是小批量梯度下降法, mini-batch gradient descent 便被提了出来。其主要思想就是每次只拿总训练集的一小部分来训练,比如一共有5000个样本,每次拿100个样本来计算loss,更新参数。50次后完成整个样本集的训练,为一轮(epoch)。由于每次更新用了多个样本来计算loss,就使得loss的计算和参数的更新更加具有代表性。不像原始SGD很容易被某一个样本给带偏 。loss的下降更加稳定,同时小批量的计算,也减少了计算资源的占用。
公式推导
我们再来回顾一下参数更新公式。每一次迭代按照一定的学习率 α \alpha α 沿梯度的反方向更新参数,直至收敛
θ t + 1 = θ t − α d f d θ \theta_{t+1}=\theta_{t}-\alpha\frac{df}{d\theta} θt+1=θt−αdθdf
接下来我们回到房价预测问题上。线形模型:
y p , i = a x i + b y_{p,i}=ax_i+b yp,i=axi+b
这是经典梯度下降方法求loss,每一个样本都要经过计算:
l o s s = 1 2 m ∑ i = 1 m ( y p , i − y i ) 2 {loss=\frac{1}{2m}\sum_{i=1}^m(y_{p,i}-y_i)^2 } loss=2m1i=1∑m(yp,i−yi)2
这是SGD梯度下降方法:
l o s s = 1 2 ( y p , i − y i ) 2 {loss=\frac{1}{2}(y_{p,i}-y_i)^2 } loss=21(yp,i−yi)2
这是mini-batch 梯度下降法, k表示每一个batch的总样本数:
l o s s b a t c h = 1 2 k ∑ i = 1 k ( y p , i − y i ) 2 {loss_{batch}=\frac{1}{2k}\sum_{i=1}^k(y_{p,i}-y_i)^2 } lossbatch=2k1i=1∑k(yp,i−yi)2
要优化的参数有两个,分别是a和b,我们分别对他们求微分,也就是偏微分, 再求和的均值
∂ l o s s b a t c h ∂ a = 1 k ∑ i = 1 k ( a x i + b − y i ) x i \frac{\partial loss_{batch}}{\partial a}=\frac{1}{k}\sum_{i=1}^k(ax_i+b-y_i)x_i ∂a∂lossbatch=k1i=1∑k(axi+b−yi)xi
∂ l o s s b a t c h ∂ b = 1 k ∑ i = 1 k ( a x i + b − y i ) \frac{\partial loss_{batch}}{\partial b}=\frac{1}{k}\sum_{i=1}^k(ax_i+b-y_i) ∂b∂lossbatch=k1i=1∑k(axi+b−yi)
∂ l o s s b a t c h ∂ a \frac{\partial loss_{batch}}{\partial a} ∂a∂lossbatch 记为 ∇ a \nabla a ∇a ∂ l o s s b a t c h ∂ b \frac{\partial loss_{batch}}{\partial b} ∂b∂lossbatch 记为 ∇ b \nabla b ∇b ,分别表示loss在a、b方向的梯度, 更新参数的方法如下
a n e w = a − α ∇ a a_{new}=a-\alpha \nabla a anew=a−α∇a
b n e w = b − α ∇ b b_{new}=b-\alpha \nabla b bnew=b−α∇b
实验
小技巧:在每一个epoch计算完所有的样本后,计算下一代样本的时候,可以选择打乱所有样本顺序。
下面是SGD方法的训练结果
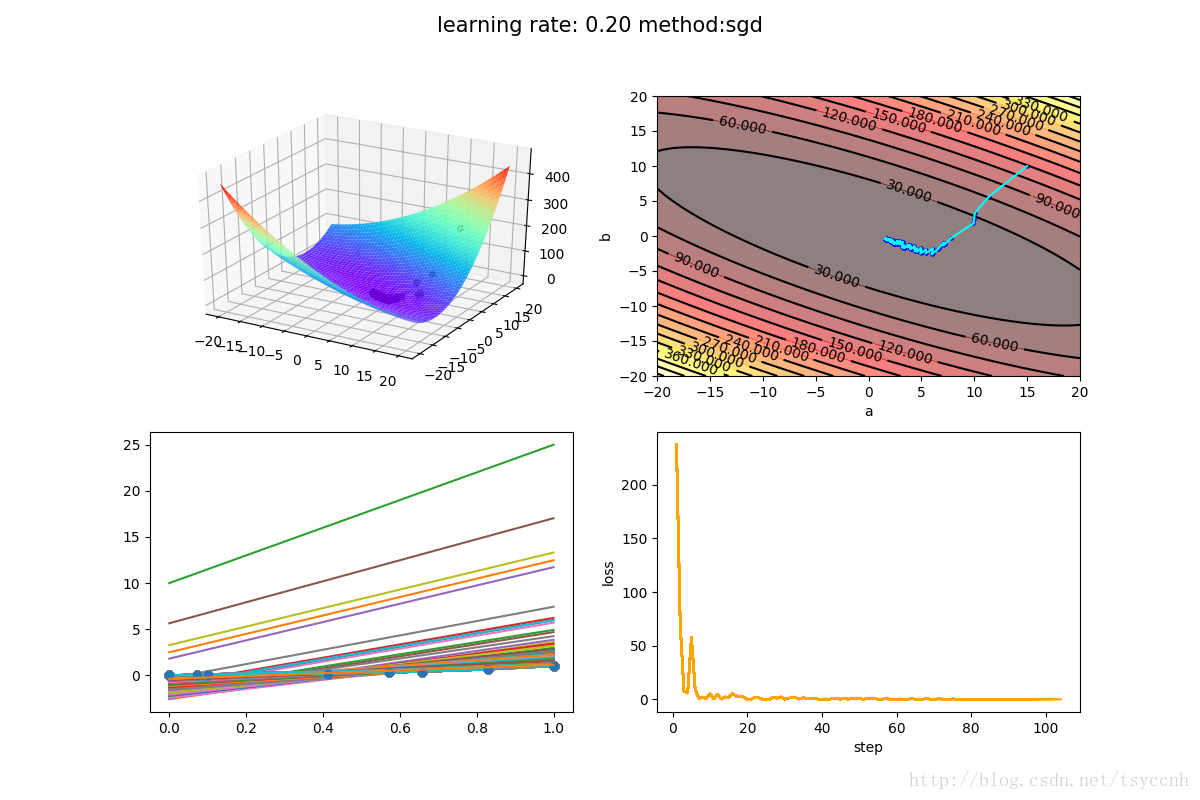
下面是 mini-batch SGD方法的训练结果

由于我的训练样本比较少,所以选择了比较大的学习率来体现效果。mini-batch SGD中,每次选择3个样本作为一个batch进行训练。容易看出,波动的减小还是比较明显。同时收敛的速度也是大大加快,几乎一步就走到了合适的参数范围。
由于mini-batch SGD 比 SGD 效果好很多,所以人们一般说SGD都指的是 mini-batch gradient descent. 大家不要和原始的SGD混淆。现在基本所有的大规模深度学习训练都是分为小batch进行训练的。
本文全部代码实现:https://github.com/tsycnh/mlbasic/blob/master/p3 minibatch SGD.py
momentum深度学习优化函数详解 momentum 动量法
SGD 随机梯度下降深度学习优化函数详解-- SGD 随机梯度下降 |

