深度学习优化函数详解系列目录

本系列课程代码，欢迎star：
https://github.com/tsycnh/mlbasic

深度学习优化函数详解（0）-- 线性回归问题
深度学习优化函数详解（1）-- Gradient Descent 梯度下降法
深度学习优化函数详解（2）-- SGD 随机梯度下降
深度学习优化函数详解（3）-- mini-batch SGD 小批量随机梯度下降
深度学习优化函数详解（4）-- momentum 动量法
深度学习优化函数详解（5）-- Nesterov accelerated gradient (NAG)
深度学习优化函数详解（6）-- adagrad

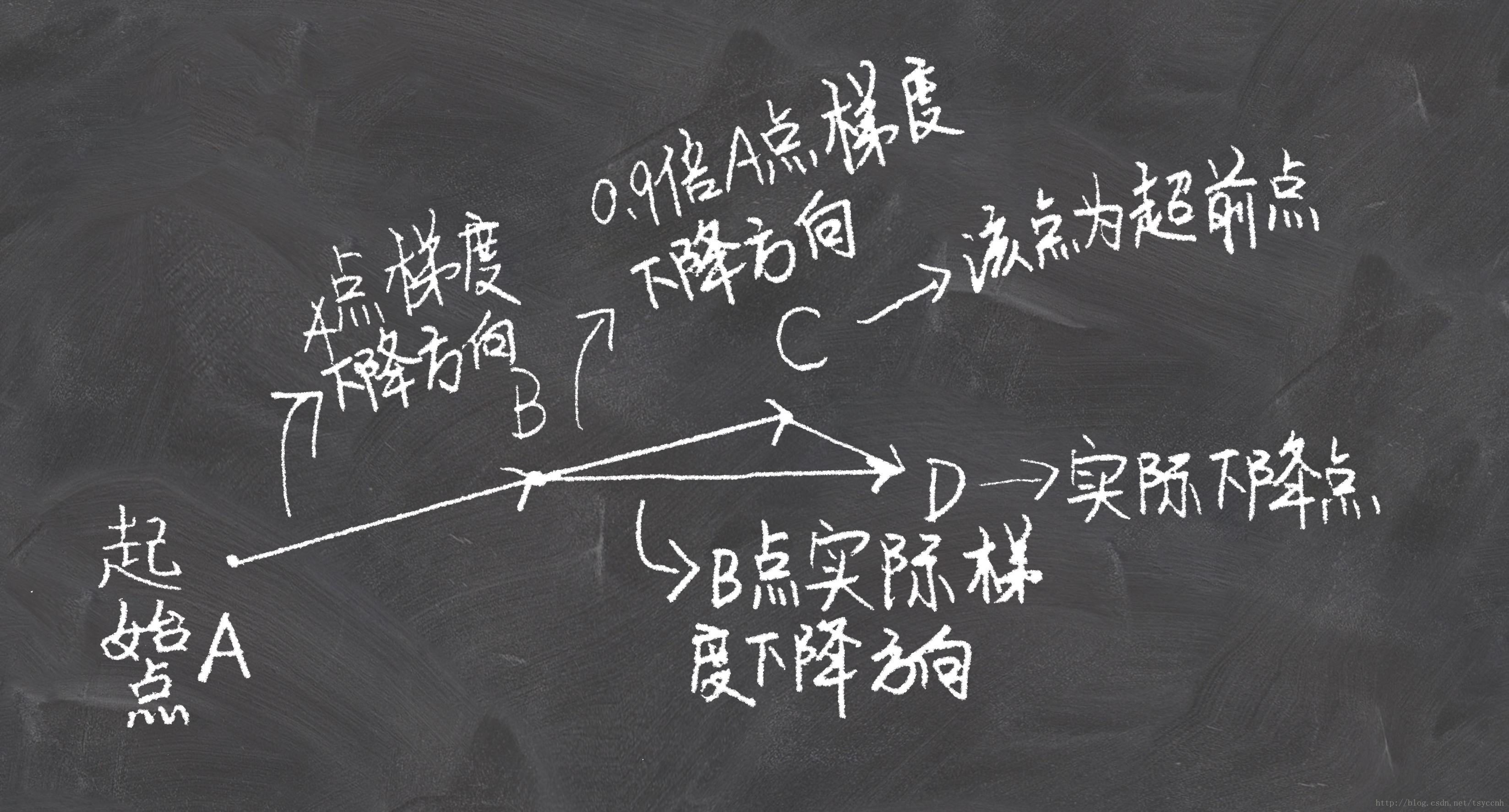
上一篇文章讲解了犹如小球自动滚动下山的动量法（momentum）这篇文章将介绍一种更加“聪明”的滚动下山的方式。动量法每下降一步都是由前面下降方向的一个累积和当前点的梯度方向组合而成。于是一位大神（Nesterov）就开始思考，既然每一步都要将两个梯度方向（历史梯度、当前梯度）做一个合并再下降，那为什么不先按照历史梯度往前走那么一小步，按照前面一小步位置的“超前梯度”来做梯度合并呢？如此一来，小球就可以先不管三七二十一先往前走一步，在靠前一点的位置看到梯度，然后按照那个位置再来修正这一步的梯度方向。如此一来，有了超前的眼光，小球就会更加”聪明“, 这种方法被命名为Nesterov accelerated gradient 简称 NAG。

↑这是momentum下降法示意图

↑这是NAG下降法示意图
看上面一张图仔细想一下就可以明白，Nesterov动量法和经典动量法的差别就在B点和C点梯度的不同。

公式推导

上图直观的解释了NAG的全部内容。
第一次看到NAG的梯度下降公式的时候我是懵的，梯度下降的流程比较明白，公式上不太理解。后来推导了好半天才得到NAG的公式，下面就把我推导的过程写出来。我推导公式的过程完全符合上面NAG的示意图，可以对比参考。
记v t v_tvt​ 为第t次迭代梯度的累积
v 0 = 0 v_0=0v0​=0
v 1 = η ∇ θ J ( θ ) v_1=\eta \nabla_{\theta}J(\theta)v1​=η∇θ​J(θ)
v 2 = γ v 1 + η ∇ θ J ( θ − γ v 1 ) v_2=\gamma v_1+\eta \nabla_{\theta}J(\theta-\gamma v_1)v2​=γv1​+η∇θ​J(θ−γv1​)
↓ \downarrow↓
v t = γ v t − 1 + η ∇ θ J ( θ − γ v t − 1 ) v_t=\gamma v_{t-1}+\eta \nabla_{\theta}J(\theta-\gamma v_{t-1})vt​=γvt−1​+η∇θ​J(θ−γvt−1​)
参数更新公式
θ n e w = θ − v t \theta_{new} = \theta - v_tθnew​=θ−vt​

公式里的− γ v t − 1 -\gamma v_{t-1}−γvt−1​ 就是图中B到C的那一段向量， θ − γ v t − 1 \theta-\gamma v_{t-1}θ−γvt−1​ 就是C点的坐标（参数）
γ \gammaγ 代表衰减率，η \etaη 代表学习率。

实验

实验选择了学习率 η = 0.01 \eta=0.01η=0.01, 衰减率 γ = 0.9 \gamma = 0.9γ=0.9

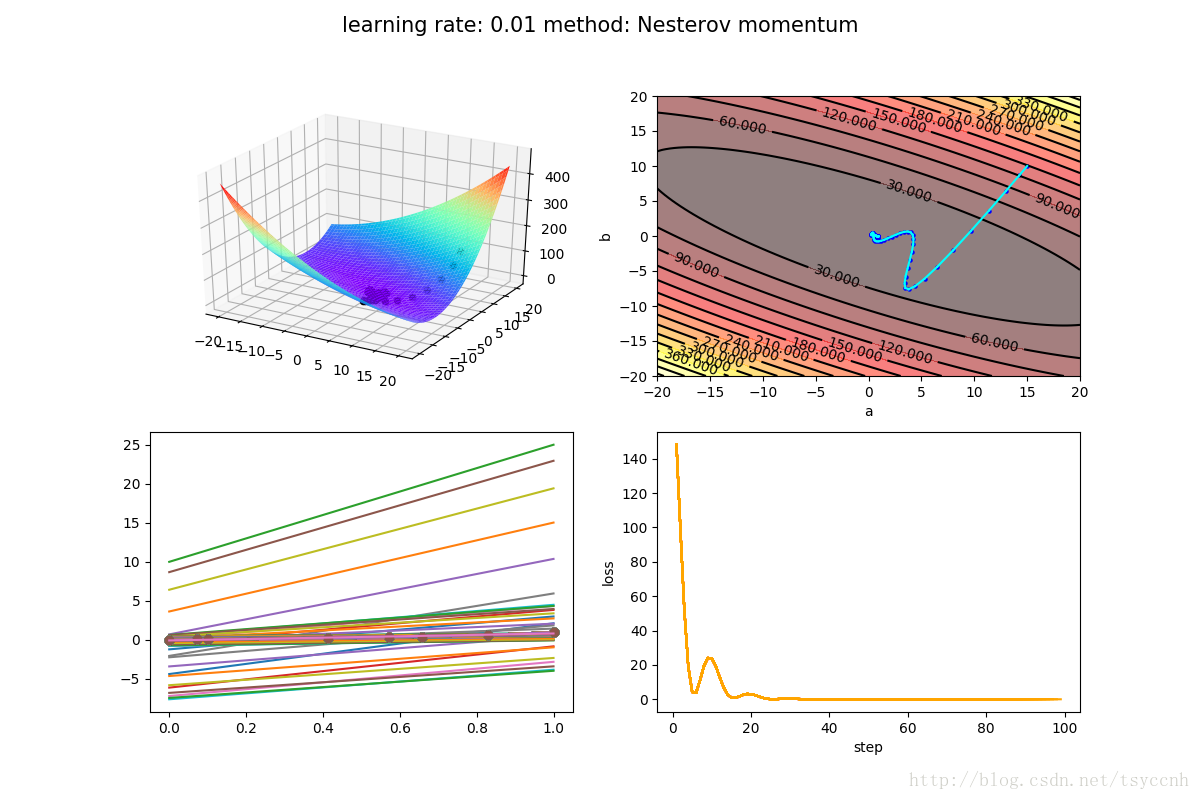
↑ 这是Nesterov方法

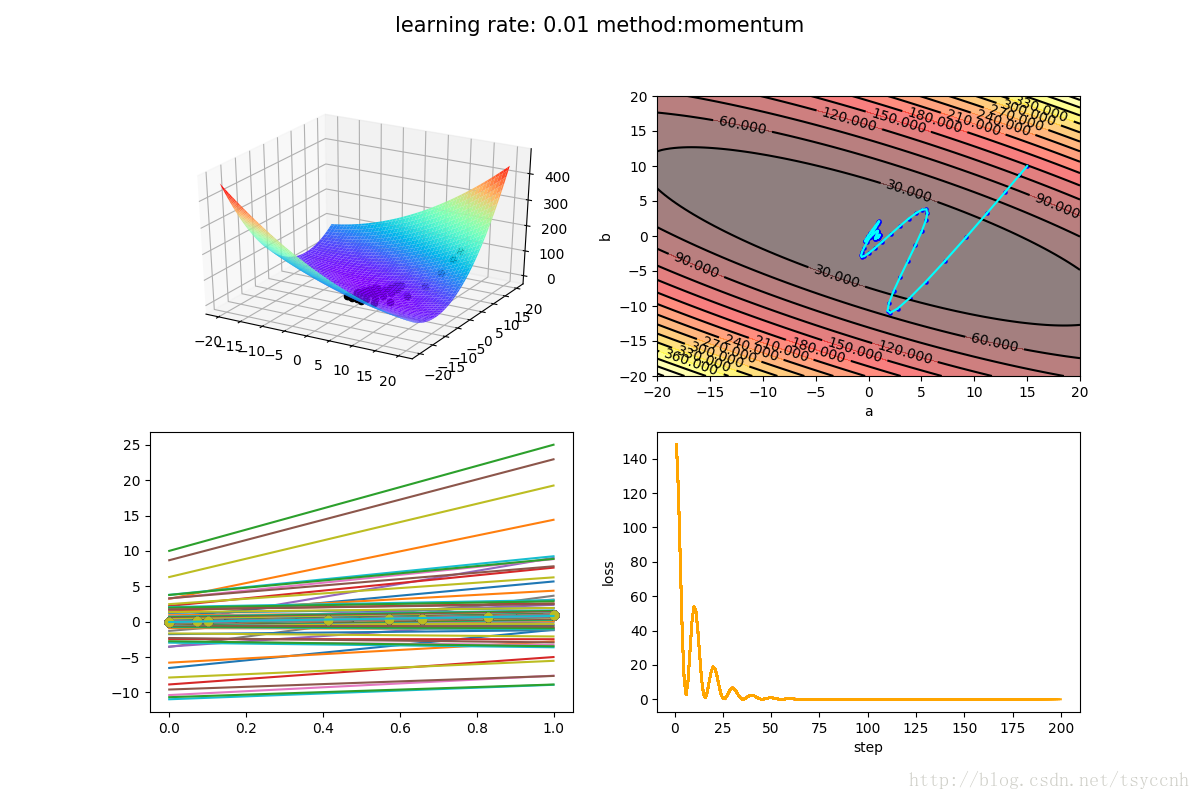
↑ 这是动量法（momentum)

没有对比就没有伤害，NAG方法收敛速度明显加快。波动也小了很多。实际上NAG方法用到了二阶信息，所以才会有这么好的结果。

实验源码下载 https://github.com/tsycnh/mlbasic/blob/master/p5 Nesterov momentum.py