LSTM是一种时间递归神经网络,它出现的原因是为了解决RNN的一个致命的缺陷。原生的RNN会遇到一个很大的问题,叫做The vanishing gradient problem for RNNs,也就是后面时间的节点会出现老年痴呆症,也就是忘事儿,这使得RNN在很长一段时间内都没有受到关注,网络只要一深就没法训练。后来有些大牛们开始使用递归神经网络来对时间关系进行建模。而根据深度学习三大牛的阐述,LSTM网络已被证明比传统的RNNS更加有效。
适合多输入变量的神经网络模型一直让开发人员很头痛,但基于(LSTM)的循环神经网络能够几乎可以完美的解决多个输入变量的问题。
基于(LSTM)的循环神经网络可以很好的利用在时间序列预测上,因为很多古典的线性方法难以适应多变量或多输入预测问题。
在本教程中,你会看到如何在Keras深度学习库中开发多变量时间序列预测的LSTM模型。
读完本教程后,你将学会:
· 如何将原始数据集转换为可用于时间序列预测的数据集。
· 如何准备数据并创建适应多变量时间序列预测问题的LSTM。
· 如何做出预测并将结果重新调整到原始单位。
本教程分为3部分:
1.空气污染预报。
2.基本数据准备。
3.多变量LSTM预测模型。
Python环境
本教程假设你已安装Python SciPy环境,你可以在本教程中使用Python 2或3。你必须使用TensorFlow或Theano后端安装Keras(2.0或更高版本)。本教程还 假设你已经安装了scikit-learn,Pandas,NumPy和Matplotlib。如果你需要帮助你的环境,请参阅这篇文章:
如何为Anaconda设置机器学习和深度学习的Python环境
空气污染预报
在这个小例子中,我们将使用空气质量数据集。这是一个数据集,在美国驻北京大使馆五年内报告天气和污染水平。数据类型包括日期时间、称为PM2.5浓度的污染物、以及天气信息、包括露点(露点温度)、温度、压力、风向、风速和累积的降雪小时数。原始数据中的完整功能列表如下:
1.NO:行号。
2.year:年。
3.month:月。
4.day:日。
5.hour:小时。
6.pm2.5:PM2.5浓度。
7.DEWP:露点温度。
8.TEMP:温度。
9.PRES:压力。
10.cbwd:风向。
11.Iws:风速。
12.ls:积雪的时间
13.Ir:累积的下雨时数
我们可以使用这些数据并构建一个预测问题,基于天气条件和前几个小时的污染,我们预测在下一个小时的污染。你可以从UCI Machine Learning Repository下载数据集—北京PM2.5数据集。下载数据集并将其放在你当前的工作目录中,文件名为“raw.csv”。
基本数据准备
第一步,我们必须清洗数据。
以下是原始数据集的前几行。
No,year,month,day,hour,pm2.5,DEWP,TEMP,PRES,cbwd,Iws,Is,Ir
1,2010,1,1,0,NA,-21,-11,1021,NW,1.79,0,0
2,2010,1,1,1,NA,-21,-12,1020,NW,4.92,0,0
3,2010,1,1,2,NA,-21,-11,1019,NW,6.71,0,0
4,2010,1,1,3,NA,-21,-14,1019,NW,9.84,0,0
5,2010,1,1,4,NA,-20,-12,1018,NW,12.97,0,0
第一步是将日期时间信息整合为一个日期时间,以便我们可以将其用作Pandas的索引。我们需要快速显示前24小时的pm2.5的NA值。因此,我们需要删除第一行数据。在数据集中还有几个分散的“NA”值;我们现在可以用0值标记它们。
以下脚本加载原始数据集,并将日期时间信息解析为Pandas Data Frame索引。“No”列被删除,然后为每列指定更清晰的名称。最后,将NA值替换为“0”值,并删除前24小时。
from pandas import read_csv
from datetime import datetime
def parse(x):
return datetime.strptime(x, '%Y %m %d %H')
dataset = read_csv('raw.csv', parse_dates = [['year', 'month', 'day', 'hour']], index_col=0, date_parser=parse)
dataset.drop('No', axis=1, inplace=True)
dataset.columns = ['pollution', 'dew', 'temp', 'press', 'wnd_dir', 'wnd_spd', 'snow', 'rain']
dataset.index.name = 'date'
dataset['pollution'].fillna(0, inplace=True)
dataset = dataset[24:]
print(dataset.head(5))
dataset.to_csv('pollution.csv')
运行该示例打印转换的数据集的前5行,并将数据集保存到“pollution.csv”。
Date pollution dew temp press wnd_dir wnd_spd snow rain
2010-01-02 00:00:00 129.0 -16 -4.0 1020.0 SE 1.79 0 0
2010-01-02 01:00:00 148.0 -15 -4.0 1020.0 SE 2.68 0 0
2010-01-02 02:00:00 159.0 -11 -5.0 1021.0 SE 3.57 0 0
2010-01-02 03:00:00 181.0 -7 -5.0 1022.0 SE 5.36 1 0
2010-01-02 04:00:00 138.0 -7 -5.0 1022.0 SE 6.25 2 0
下面的代码加载了“ pollution.csv ”文件,并将每个系列作为单独的子图绘制,除了风速dir,这是分类的。
from pandas import read_csv
from matplotlib import pyplot
# load dataset
dataset = read_csv('pollution.csv', header=0, index_col=0)
values = dataset.values
# specify columns to plot
groups = [0, 1, 2, 3, 5, 6, 7]
i = 1
# plot each column
pyplot.figure()
for group in groups:
pyplot.subplot(len(groups), 1, i)
pyplot.plot(values[:, group])
pyplot.title(dataset.columns[group], y=0.5, loc='right')
i += 1
pyplot.show()
运行示例创建一个具有7个子图的程序,显示每个变量的5年数据。
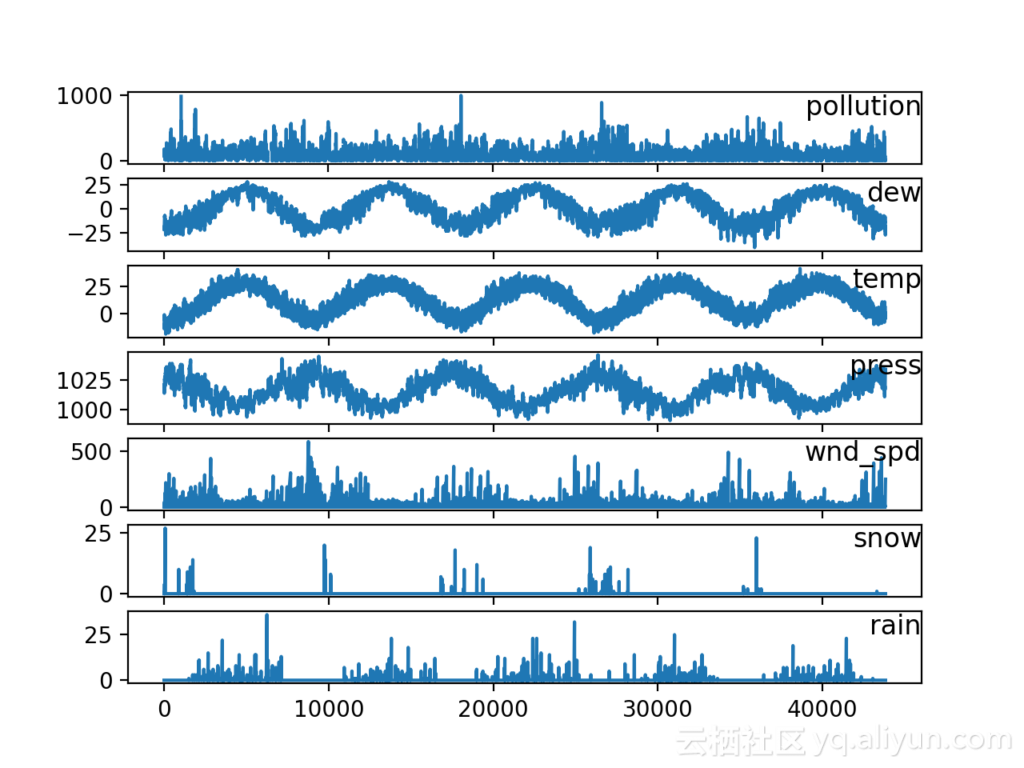
多变量LSTM预测模型建立:
LSTM数据准备
第一步是为LSTM准备污染数据集。这涉及将数据集视为监督学习问题并对输入变量进行归一化处理。考虑到上一个时间段的污染测量和天气条件,我们将把监督学习问题作为预测当前时刻(t)的污染情况。根据过去24小时的天气情况和污染,预测下一个小时的污染,并给予下一个小时的“预期”天气条件。
我们可以使用在博客中开发的series_to_supervised()函数来转换数据集:如何将时间序列转换为Python中的监督学习问题
首先,加载“ pollution.csv ”数据集。风速特征是标签编码(整数编码)。如果你有兴趣探索,也可以使用热编码。
接下来,所有功能都被规范化,然后将数据集转换为监督学习问题。然后删除要预测的小时的天气变量(t)。
完整的代码清单如下:
def series_to_supervised(data, n_in=1, n_out=1, dropnan=True):
n_vars = 1 if type(data) is list else data.shape[1]
df = DataFrame(data)
cols, names = list(), list()
for i in range(n_in, 0, -1):
cols.append(df.shift(i))
names += [('var%d(t-%d)' % (j+1, i)) for j in range(n_vars)]
for i in range(0, n_out):
cols.append(df.shift(-i))
if i == 0:
names += [('var%d(t)' % (j+1)) for j in range(n_vars)]
else:
names += [('var%d(t+%d)' % (j+1, i)) for j in range(n_vars)]
agg = concat(cols, axis=1)
agg.columns = names
if dropnan:
agg.dropna(inplace=True)
return agg
dataset = read_csv('pollution.csv', header=0, index_col=0)
values = dataset.values
encoder = LabelEncoder()
values[:,4] = encoder.fit_transform(values[:,4])
values = values.astype('float32')
scaler = MinMaxScaler(feature_range=(0, 1))
scaled = scaler.fit_transform(values)
reframed = series_to_supervised(scaled, 1, 1)
reframed.drop(reframed.columns[[9,10,11,12,13,14,15]], axis=1, inplace=True)
print(reframed.head())
运行示例打印转换后的数据集的前5行。我们可以看到8个输入变量(输入序列)和1个输出变量(当前小时的污染水平)。
var1(t-1) var2(t-1) var3(t-1) var4(t-1) var5(t-1) var6(t-1) \
1 0.129779 0.352941 0.245902 0.527273 0.666667 0.002290
2 0.148893 0.367647 0.245902 0.527273 0.666667 0.003811
3 0.159960 0.426471 0.229508 0.545454 0.666667 0.005332
4 0.182093 0.485294 0.229508 0.563637 0.666667 0.008391
5 0.138833 0.485294 0.229508 0.563637 0.666667 0.009912
var7(t-1) var8(t-1) var1(t)
1 0.000000 0.0 0.148893
2 0.000000 0.0 0.159960
3 0.000000 0.0 0.182093
4 0.037037 0.0 0.138833
5 0.074074 0.0 0.109658
注意:我们必须提供超过一小时的输入时间步长。因为在解决序列预测问题时,LSTMs通过时间进行反向传播。
定义和拟合模型
在本节中,我们将通过多变量输入数据拟合LSTM。
首先,我们必须将准备好的数据集分成训练集和测试集。为了加快对这次示范模型的训练,我们将仅使用第一年的数据来拟合模型,然后对其余4年的数据进行评估。下面的示例将数据集分成训练集和测试集,然后将训练集和测试集分成输入和输出变量。最后,将输入(X)重构为LSTM预期的3D格式,即[样本,时间步长,特征]。
# split into train and test sets
values = reframed.values
n_train_hours = 365 * 24
train = values[:n_train_hours, :]
test = values[n_train_hours:, :]
# split into input and outputs
train_X, train_y = train[:, :-1], train[:, -1]
test_X, test_y = test[:, :-1], test[:, -1]
# reshape input to be 3D [samples, timesteps, features]
train_X = train_X.reshape((train_X.shape[0], 1, train_X.shape[1]))
test_X = test_X.reshape((test_X.shape[0], 1, test_X.shape[1]))
print(train_X.shape, train_y.shape, test_X.shape, test_y.shape)
运行此示例打印训练集的形状:
(8760, 1, 8) (8760,) (35039, 1, 8) (35039,)
现在我们可以定义和拟合我们的LSTM模型。
我们将在第一个隐层中定义具有50个神经元的LSTM和用于预测污染的输出层中的1个神经元。输入形状是1个时间步长,具有8个特征。
我们将在我们的模型中使用平均绝对误差(MAE)损失函数。该模型将拟合50个批量大小为72的训练时期。最后,我们通过在fit()函数中设置validation_data参数来跟踪训练过程中的训练和测试失败。在运行结束时,绘制训练和测试损失。
# design network
model = Sequential()
model.add(LSTM(50, input_shape=(train_X.shape[1], train_X.shape[2])))
model.add(Dense(1))
model.compile(loss='mae', optimizer='adam')
# fit network
history = model.fit(train_X, train_y, epochs=50, batch_size=72, validation_data=(test_X, test_y), verbose=2, shuffle=False)
# plot history
pyplot.plot(history.history['loss'], label='train')
pyplot.plot(history.history['val_loss'], label='test')
pyplot.legend()
pyplot.show()
评估模型
模型拟合后,我们可以预测整个测试数据集。
我们将预测的数据集与测试数据集相结合,并反演缩放。我们还可以用预期的污染数字来反演测试数据集的缩放。使用预测值和实际值,我们可以计算模型的误差分数。并且我们还可以计算出与变量本身相同的单位产生误差的均方根误差(RMSE)。
完整例子
完整的示例如下所示:源程序附件中下载!
运行示例首先创建一个绘图,显示训练中的训练损失和测试损失:
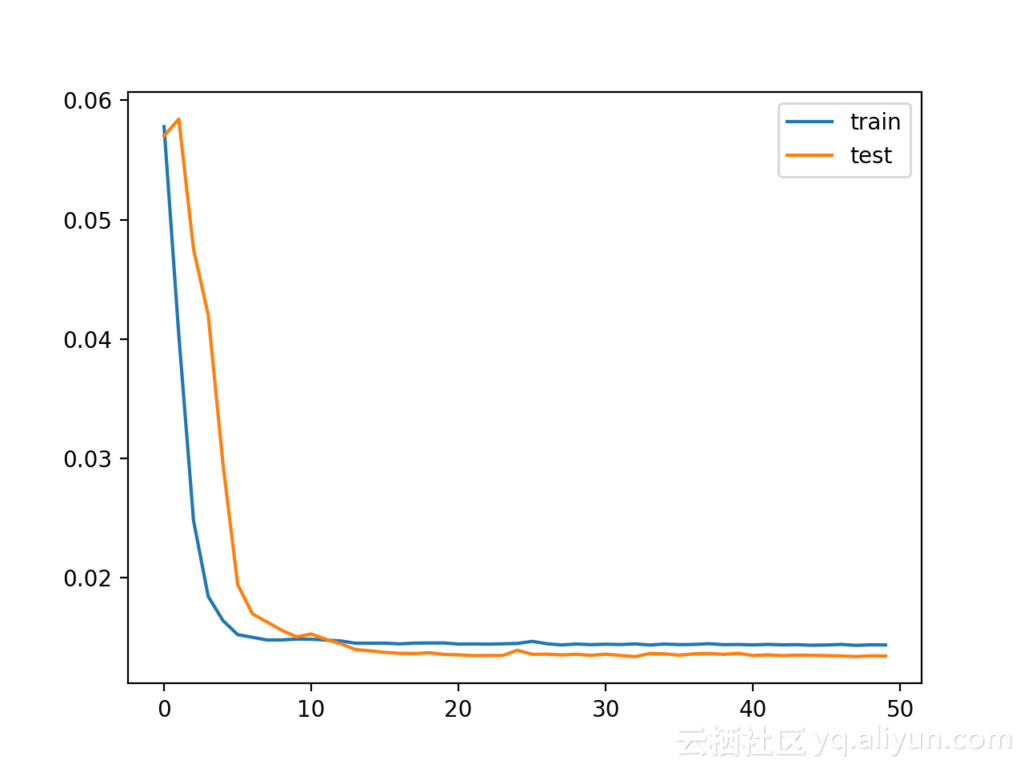
有趣的是,我们可以看到测试损失低于训练损失,该模型可能过度拟合训练数据。
训练损失和测试损失在每个训练时期结束时打印。在运行结束时,打印测试数据集上模型的最终RMSE。我们可以看到,该模型实现了可观的RMSE:3.836。
Epoch 46/50
0s - loss: 0.0143 - val_loss: 0.0133
Epoch 47/50
0s - loss: 0.0143 - val_loss: 0.0133
Epoch 48/50
0s - loss: 0.0144 - val_loss: 0.0133
Epoch 49/50
0s - loss: 0.0143 - val_loss: 0.0133
Epoch 50/50
0s - loss: 0.0144 - val_loss: 0.0133
Test RMSE: 3.836

